ESERCIZIO 1; FILA A

$2cosx#-1=0$

ESERCIZIO del tipo Atrig(x)+B=0

Risoluzione corretta:

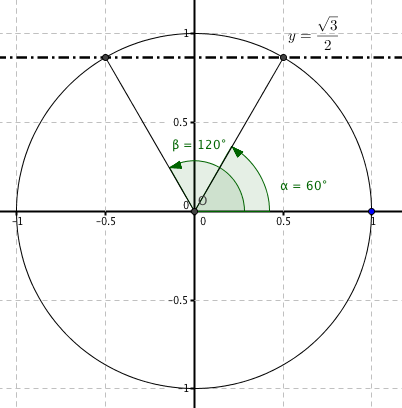
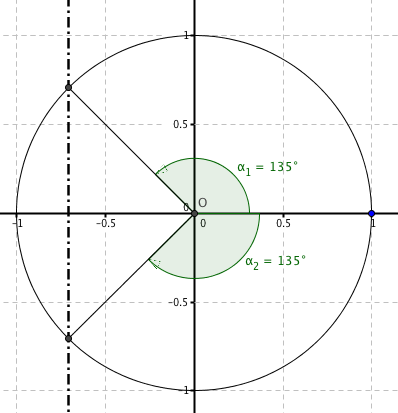
Portiamo in forma di equazione goniometrica elementare e facciamo il grafico:

$2cosx-1 = 0$
$2cosx= +1$
$cosx=+1/2$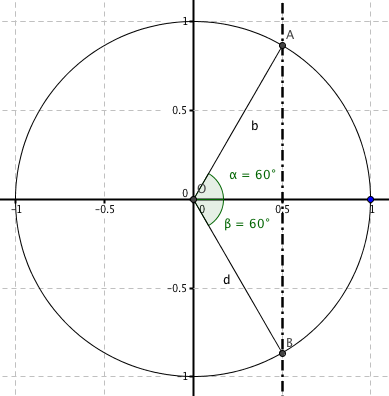

Per ispezione le due serie di soluzioni sono le seguenti:

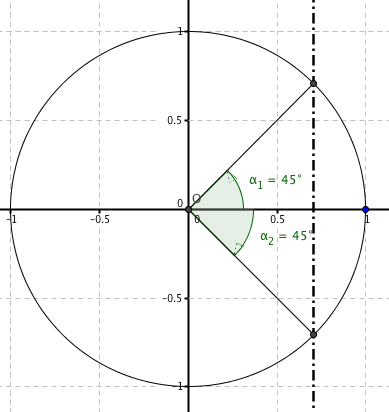
$(x=60°+k360°)vv(x=-60°+k360°)$

che si possono scrivere anche:

$x=+-60°+k360°$

OPPURE (in radianti):

$(x=pi/3+2kpi)vv(x=-pi/3+2kpi)$

che si possono scrivere anche:

$x=+-pi/3+2kpi;$

OPPURE :

$(x=pi/3+2kpi)vv(x=5/3+2kpi)$

I quattro rettangoli sopra sono modi diversi di scrivere la stessa soluzione.
valutazione: 1

Soluzione non corretta di tipo 1 (errata soluzione della eq. goniom. elem.)
arrivato a $cosx = 1/2$ deduce (non compare il grafico)

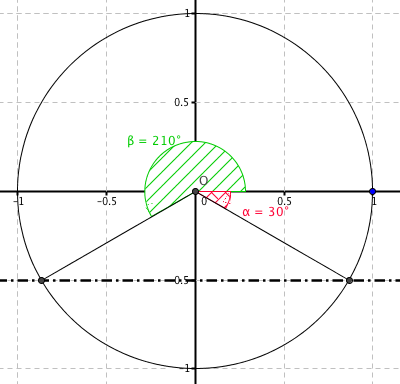
$(x=pi/3+2kpi;)vv(x=2/3pi+2kpi;)$

analisi dell'errore: forse una volta trovato correttamente il primo angolo ($pi/3$), ha poi preso l'angolo "sinistro" nel secondo quadrante anziche' quello "inferiore" nel quarto quadrante,
con il disegno come in figura sarebbe risultato abbastanza improbabile fare questo errore

ESERCIZIO 1; FILA B

$2sinx #-1=0$

ESERCIZIO del tipo Atrig(x)+B=0

Risoluzione corretta:

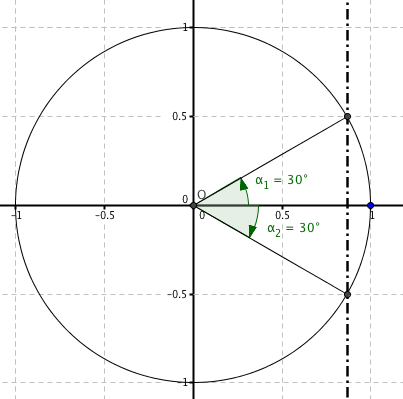
Portiamo in forma di equazione goniometrica elementare e facciamo il grafico:

$2sinx-1 = 0$
$2sinx= +1$
$sinx=+1/2$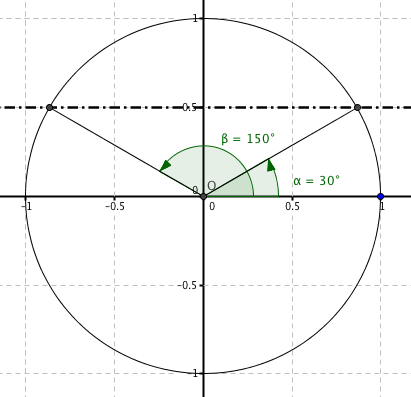

Per ispezione le due serie di soluzioni sono le seguenti:

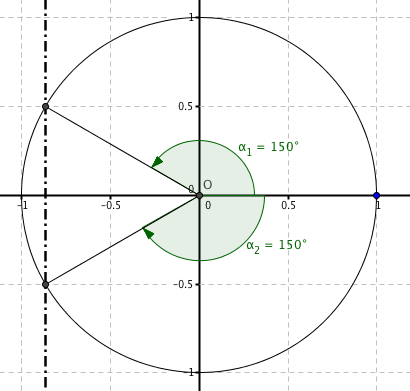
$(x=30°+k360°)vv(x=150°+k360°)$

OPPURE (in radianti):

$(x=pi/6+2kpi)vv(x=5/6+2kpi)$

I due rettangoli sopra sono modi diversi di scrivere la stessa soluzione.

Soluzione non corretta di tipo 1 (errata soluzione della eq. goniom. elem.)
arrivato a $sinx = 1/2$ deduce (non compare il grafico)

$x=pi/2+2kpi;$

ESERCIZIO 2; FILA A/B

$sinx=sqrt(3)/2$

ESERCIZIO del tipo trig(x)=A

Risoluzione corretta:

Per ispezione le due serie di soluzioni sono le seguenti:

$(x=60°+k360°)vv(x=120°+k360°)$

OPPURE (in radianti):

$(x=pi/3+2kpi)vv(x=2/3pi+2kpi)$

valutazione: 1

ESERCIZIO 3; FILA A

$cosx=-sqrt(2)/2$

ESERCIZIO del tipo trig(x)=A

Risoluzione corretta:

Per ispezione le due serie di soluzioni sono le seguenti:

$(x=135°+k360°)vv(x=-135°+k360°)$

OPPURE

$(x=+-135°+k360°)$

OPPURE (in radianti):

$(x=3/4pi+2kpi)vv(x=-3/4pi+2kpi)$

OPPURE

$(x=+-3/4pi+2kpi)$

OPPURE:

$(x=3/4pi+2kpi)vv(x=5/4pi+2kpi)$

valutazione: 1

ESERCIZIO 3; FILA B

$cosx=-1/2$

ESERCIZIO del tipo trig(x)=A

Risoluzione corretta:

Per ispezione le due serie di soluzioni sono le seguenti:

$(x=120°+k360°)vv(x=-120°+k360°)$

OPPURE

$(x=+-120°+k360°)$

OPPURE (in radianti):

$(x=2/3pi+2kpi)vv(x=-2/3pi+2kpi)$

OPPURE

$(x=+-2/3pi+2kpi)$

OPPURE:

$(x=2/3pi+2kpi)vv(x=4/3pi+2kpi)$

valutazione: 1

ESERCIZIO 4; FILA A

$2cos3x-sqrt(3)=0$

ESERCIZIO del tipo Atrig(Bx)+C=0 da risolvere tramite sostituzione dell'argomento (tipicamente con una variabile di comodo chiamata $alpha$)

Risoluzione corretta:

Portiamo in forma di equazione goniometrica elementare e facciamo il grafico:

$2cos3x-sqrt(3)=0$

$2cos3x= +sqrt(3)$

$cos3x=sqrt(3)/2$

$cosalpha=sqrt(3)/2$
questa eq. goniom. elem. porta a due serie di soluzioni in $alpha$ che possiamo chiamare serie $alpha_1$ e serie $alpha_2$

$(alpha_1=30°+k360°)vv(alpha_2=-30°+k360°)$

OPPURE

$(alpha_1=pi/6+2kpi)vv(alpha_2=-pi/6+2kpi)$

Ma queste sono soluzioni in $alpha$ e bisogna tornare in x

$alpha_1=3x$
$3x=alpha_1=pi/6+2kpi$
$3x=pi/6+2kpi$
$x=pi/18+2/3kpi$

$alpha_2=3x$
$3x=alpha_2=-pi/6+2kpi$
$3x=-pi/6+2kpi$
$x=-pi/18+2/3kpi$

Sintetizzabili in

$x=+-pi/18+2/3kpi$

altra strada avrebbe potuto essere la seguente:

$(alpha_1=pi/6+2kpi)vv(alpha_2=11/6pi+2kpi)$

Ma queste sono soluzioni in $alpha$ e bisogna tornare in x

$alpha_1=3x$
$3x=alpha_1=pi/6+2kpi$
$3x=pi/6+2kpi$
$x=pi/18+2/3kpi$
$alpha_2=3x$
$3x=alpha_2=11/6pi+2kpi$
$3x=11/6pi+2kpi$
$x=11/18pi+2/3kpi$

in questo caso la soluzione alla soluzione sarebbe stata:
$(x=pi/18+2/3kpi)vv(x=11/18pi+2/3kpi)$

valutazione: 1

ESERCIZIO 4; FILA B

$2cos3x-sqrt(3)=0$

ESERCIZIO del tipo Atrig(Bx)+C=0 da risolvere tramite sostituzione dell'argomento (tipicamente con una variabile di comodo chiamata $alpha$)

Risoluzione corretta:

Portiamo in forma di equazione goniometrica elementare e facciamo il grafico:

$2cos3x+sqrt(3)=0$

$2cos3x= -sqrt(3)$

$cos3x=-sqrt(3)/2$

$cosalpha=-sqrt(3)/2$
questa eq. goniom. elem. porta a due serie di soluzioni in $alpha$ che possiamo chiamare serie $alpha_1$ e serie $alpha_2$

$(alpha_1=150°+k360°)vv(alpha_2=-150°+k360°)$

OPPURE

$(alpha_1=150°+k360°)vv(alpha_2=210°+k360°)$

OPPURE

$(alpha_1=5/6pi+2kpi)vv(alpha_2=-5/6+2kpi)$

OPPURE
$(alpha_1=5/6pi+2kpi)vv(alpha_2=7/6+2kpi)$

OPPURE
Ma queste sono soluzioni in $alpha$ e bisogna tornare in x

$alpha_1=3x$
$3x=alpha_1=5/6pi+2kpi$
$3x=5/6pi+2kpi$
$x=5/18pi+2/3kpi$

$alpha_2=3x$
$3x=alpha_2=-5/6pi+2kpi$
$3x=-5/6pi+2kpi$
$x=-5/18pi+2/3kpi$

Sintetizzabili in

$x=+-5/18pi+2/3kpi$

altra strada avrebbe potuto essere la seguente:

$(alpha_1=5/6pi+2kpi)vv(alpha_2=7/6pi+2kpi)$

Ma queste sono soluzioni in $alpha$ e bisogna tornare in x

$alpha_1=3x$
$3x=alpha_1=5/6pi+2kpi$
$3x=5/6+2kpi$
$x=5/18pi+2/3kpi$
$alpha_2=3x$
$3x=alpha_2=7/6pi+2kpi$
$3x=7/6pi+2kpi$
$x=7/18pi+2/3kpi$

in questo caso la soluzione alla soluzione sarebbe stata:
$(x=5/18pi+2/3kpi)vv(x=7/18pi+2/3kpi)$

valutazione: 1

ESERCIZIO 5; FILA A

$2sin(x-30°)+1=0$

ESERCIZIO del tipo Atrig(x+B)+C=0 da risolvere tramite sostituzione dell'argomento (tipicamente con una variabile di comodo chiamata $alpha$)

Risoluzione corretta:

Portiamo in forma di equazione goniometrica elementare e facciamo il grafico:

$2sin(x-30°)=-1$

$sin(x-30°)=-1/2$

facciamo l'apposizione $alpha=x-30°$

$sin(alpha)=-1/2$
questa eq. goniom. elem. porta a due serie di soluzioni in $alpha$ che possiamo chiamare serie $alpha_1$ e serie $alpha_2$

$(alpha_1=210°+k360°)vv(alpha_2=-30°+k360°)$

OPPURE (considerando che $alpha_1=210°((2pi)/(360°))=21°((2pi)/(36°))=((42°pi)/(36°))=((42pi)/(36))=(21/18 pi)=(7/6 pi)$
e che $-30°=-pi/6$
$(alpha_1=7/6+2kpi)vv(alpha_2=-pi/6+2kpi)$

Ma queste sono soluzioni in $alpha$ e bisogna tornare in x

${(alpha_1= 210 °+k360°), (alpha_1=x-30°):}

$darr

$ $x-30°=210°+k360°$

QUINDI

$x_1=240°+k360°$

anche scrivibile ($pi/3= 60 °$)

$x_1=4/3pi+2kpi$

${(alpha_2= -30 °+k360°), (alpha_2=x-30°):}

$darr

$ $x-30°=-30°+k360°$

QUINDI

$x_2=0°+k360°$
cioe'
$x_2=k360°$

anche scrivibile

$x_2=2kpi$

La soluzione e' quindi:

$(x=240°+k360°)vv(x=k360°$)

anche scrivibile

$(x=4/3 pi + 2kpi)vv(x=2kpi$)

ESERCIZIO 5; FILA B

$2sin(x-20°)+1=0$

ESERCIZIO del tipo Atrig(x+B)+C=0 da risolvere tramite sostituzione dell'argomento (tipicamente con una variabile di comodo chiamata $alpha$)

Risoluzione corretta:

Portiamo in forma di equazione goniometrica elementare e facciamo il grafico:

$2sin(x-20°)=-1$

$sin(x-20°)=-1/2$

facciamo l'apposizione $alpha=x-20°$

$sin(alpha)=-1/2$
questa eq. goniom. elem. porta a due serie di soluzioni in $alpha$ che possiamo chiamare serie $alpha_1$ e serie $alpha_2$

$(alpha_1=210°+k360°)vv(alpha_2=-30°+k360°)$

OPPURE (considerando che $alpha_1=210°((2pi)/(360°))=21°((2pi)/(36°))=((42°pi)/(36°))=((42pi)/(36))=(21/18 pi)=(7/6 pi)$
e che $-30°=-pi/6$
$(alpha_1=7/6+2kpi)vv(alpha_2=-pi/6+2kpi)$

Ma queste sono soluzioni in $alpha$ e bisogna tornare in x

${(alpha_1= 210 °+k360°), (alpha_1=x-20°):}

$darr

$ $x-20°=210°+k360°$

QUINDI

$x_1=230°+k360°$

anche scrivibile ($pi/18 = 10 °$)

$x_1=23/18pi+2kpi$

${(alpha_2= -30 °+k360°), (alpha_2=x-20°):}

$darr

$ $x-20°=-30°+k360°$

QUINDI

$x_2=-10°+k360°$

anche scrivibile ($pi/18 = 10 °$)

$x_2=-pi/18 +2kpi$

La soluzione e' quindi:

$(x=230°+k360°)vv(x=-10°+k360°$)

o in modo equivalente

$(x=230°+k360°)vv(x=350°+k360°$)

anche scrivibile

$(x=23/18pi+2kpi)vv(x=-pi/18 +2kpi$)

anche scrivibile (considerando che $2pi=36/18 pi$
e che $36/18-23/18=13/18$ cioe'
che mancano $18/13pi$ a chiudere il giro

$(x=-13/18pi+2kpi)vv(x=-pi/18 +2kpi)$

ESERCIZIO 6; FILA A

$4sin^2 x=2$

ESERCIZIO del tipo $Atrig^2(x)=C$ da risolvere tramite sostituzione della funzione goniometrica , tipicamente chiamata t, in questo caso portera' a $t^2="valore positivo"$ cioe' $t=+- sqrt("valore positivo")$ da riportare poi nella variabile x)

Risoluzione corretta:

Portiamo in forma di equazione goniometrica elementare in t
$4sin^2 x=2$

$sin^2 x=2/4$

$sin^2 x=1/2$

facciamo l'apposizione t=sin x

$t^2=1/2$ (Equazione di secondo grado in t)

Questa equazione di secondo grado HA DUE SOLUZIONI

$t_(1,2)=+-sqrt(1/2)$ che corrisponde a

$t_(1,2)=+-1/sqrt(2)$ che razionalizziamo

$t_(1,2)=+-1/sqrt(2) sqrt(2)/sqrt(2)$ ottenendo

$t_(1,2)=+-sqrt(2)/2$
torniamo in x

$(sin(x)=t_1 )vv (sin(x)=t_2)$

cioe'

$(sin(x)=+sqrt(2)/2 )vv (sin(x)=-sqrt(2)/2)$
Facciamo due grafici uno relativo ai seni positivi l'altro a quelli negativi

Le cui soluzioni sono
Per i seni positivi:
$x_1=pi/4+2kpi $ e $x_2=3/4 pi+2kpi$
Per i seni negativi:
$x_3=-pi/4+2kpi$ e $x_4=-3/4 pi+2kpi $
Complessivamente le quattro serie di soluzioni sono le seguenti:

$(x=+-pi/4+2kpi ) vv (x=+-3/4 pi+2kpi) $ (nota: sono stati tolti i pedici)

Sovrapponendo i due grafici noteremmo che le quattro soluzioni sono tutte separate da un angolo di $90°$
quindi e' possibile scrivere

$(x=pi/4+kpi/2 ) $

che include tutte e quattro le serie di soluzioni (la periodicita' e' pero' adesso di $pi/2$ e questo genera 4 volte piu' soluzioni al giro di quante non se ne sarebbero generate usando una periodicita' $2pi$ e questo spiega la "scomparsa" apparente di soluzioni.

ESERCIZIO 6; FILA B

$4cos^2 x=2$

Risoluzione corretta:

Portiamo in forma di equazione goniometrica elementare in t
$4cos^2 x=2$

$cos^2 x=2/4$

$cis^2 x=1/2$

facciamo l'apposizione t=cos x

$t^2=1/2$ (Equazione di secondo grado in t)

Questa equazione di secondo grado HA DUE SOLUZIONI

$t_(1,2)=+-sqrt(1/2)$ che corrisponde a

$t_(1,2)=+-1/sqrt(2)$ che razionalizziamo

$t_(1,2)=+-1/sqrt(2) sqrt(2)/sqrt(2)$ ottenendo

$t_(1,2)=+-sqrt(2)/2$
torniamo in x

$(cos(x)=t_1 )vv (cos(x)=t_2)$

cioe'

$(cos(x)=+sqrt(2)/2 )vv (cos(x)=-sqrt(2)/2)$
Facciamo due grafici uno relativo ai coseni positivi l'altro a quelli negativi

Le cui soluzioni sono
Per i coseni positivi:
$x_1=pi/4+2kpi $ e $x_2=-pi/4 +2kpi$
Per i coseni negativi:
$x_3=3/4 pi+2kpi$ e $x_4=- 3/4 pi+2kpi $
Complessivamente le quattro serie di soluzioni sono le seguenti:

$(x=+-pi/4+2kpi ) vv (x=+-3/4 pi+2kpi) $ (nota: sono stati tolti i pedici)

Sovrapponendo i due grafici noteremmo che le quattro soluzioni sono tutte separate da un angolo di $90°$
quindi e' possibile scrivere

$(x=pi/4+kpi/2 ) $

ESERCIZIO 7; FILA A

$3(3-cosx)-sin^2x=0$

ESERCIZIO del tipo $A"trig"^2(x)+ B "trig"(x)+ C=0$ con funzioni goniometriche diverse: bisogna usare $sin^2x+cos^2x=1$ per portare tutto in coseno o tutto in seno

(A): $3(3-cosx)-sin^2x=0$
$9-3cosx-sin^2x=0$ (usiamo $sin^2x=1-cos^2x$ )
$9-3cosx-(1-cos^2x)=0$
$9-3cosx-1+cos^2x=0$
$8-3cosx+cos^2x=0$
(B): $cos^2x-3cosx+8=0$

passiamo in t
(C): $t^2-3t+8=0$

Nota: l'eq. (C) e' solo una riscrittura della (B)
che e' a sua volta equivalente (nel senso che ha lo stesso insieme di soluzioni) della (A):
Se non ci fossero soluzioni nella (C) anche la (A) non avrebbe soluzioni (essendo equivalenti)

Cerchiamo le soluzioni della (C)

$t_(1,2)=(3+-sqrt(9-32))/(2)$
Il numero sotto radice e' negativo quindi (C) non ha soluzioni reali e quindi neanche (A)
soluzione dell'esercizio:

NON ESISTONO SOLUZIONI REALI (IMPOSSIBILE)

ESERCIZIO 7; FILA A

$sin^2x=3(3-cosx)$

ESERCIZIO del tipo $A"trig"^2(x)+ B "trig"(x)+ C=0$ con funzioni goniometriche diverse: bisogna usare $sin^2x+cos^2x=1$ per portare tutto in coseno o tutto in seno

(A): $sin^2x=3(3-cosx)$
$sin^2x=9-3cosx$
$-9+3cosx-sin^2x=0$ (moltiplichiamo per -1 entrambi i membri dell'equazione)
$9-3cosx+ sin^2x=0$(usiamo $sin^2x=1-cos^2x$ )
$9-3cosx-(1-cos^2x)=0$
$9-3cosx-1+cos^2x=0$
$8-3cosx+cos^2x=0$
(B): $cos^2x-3cosx+8=0$

passiamo in t
(C): $t^2-3t+8=0$

Nota: l'eq. (C) e' solo una riscrittura della (B)
che e' a sua volta equivalente (nel senso che ha lo stesso insieme di soluzioni) della (A):
Se non ci fossero soluzioni nella (C) anche la (A) non avrebbe soluzioni (essendo equivalenti)

Cerchiamo le soluzioni della (C)

$t_(1,2)=(3+-sqrt(9-32))/(2)$
Il numero sotto radice e' negativo quindi (C) non ha soluzioni reali e quindi neanche (A)
soluzione dell'esercizio:

NON ESISTONO SOLUZIONI REALI (IMPOSSIBILE)

ESERCIZIO 8; FILA A

$3cosx-2sin^2x=0$

ESERCIZIO del tipo $A"trig"^2(x)+ B "trig"(x)+ C=0$ con funzioni goniometriche diverse: bisogna usare $sin^2x+cos^2x=1$ per portare tutto in coseno o tutto in seno

$3cosx-2sin^2x=0$ (usiamo $sin^2x=1-cos^2x$ )
$3cosx-2(1-cos^2x)=0$
$3cosx-2+2cos^2x=0$
$2cos^2x+ 3cosx-2=0$

passiamo in t (t=cosx)
$2t^2+ 3t-2+=0$

$t_(1,2)=(-3+-sqrt(9+16))/(4)=(-3+-sqrt(25))/(4)=(-3+-5)/(4)={1/2,-2}$
la soluzione $t_2=-2$ non produce soluzioni in quanto la eq. goniom. elementare associata non ha soluzioni:
cosx=-2 non ha soluzioni
viceversa
la soluzione $t_1=1/2$ tornando in x diventa
cosx=1/2 (vedi esercizio 1 fila A)
che ha soluzione

$x=+-pi/3+2kpi;$

OPPURE :

$(x=pi/3+2kpi)vv(x=5/3+2kpi)$

ESERCIZIO 8; FILA B

$2sin^2x-3cosx=0$

ESERCIZIO del tipo $A"trig"^2(x)+ B "trig"(x)+ C=0$ con funzioni goniometriche diverse: bisogna usare $sin^2x+cos^2x=1$ per portare tutto in coseno o tutto in seno

$2sin^2x-3cosx-=0$ (usiamo $sin^2x=1-cos^2x$ )
$2(1-cos^2x)-3cosx=0$
$2-2cos^2x3cosx-=0$
$-2cos^2x- 3cosx+2=0$ (cambiamo di segno al tutto)
$2cos^2x+ 3cosx-2=0$

passiamo in t (t=cosx)
$2t^2+ 3t-2=0$

$t_(1,2)=(-3+-sqrt(9+16))/(4)=(-3+-sqrt(25))/(4)=(-3+-5)/(4)={1/2,-2}$
la soluzione $t_2=-2$ non produce soluzioni in quanto la eq. goniom. elementare associata non ha soluzioni:
cosx=-2 non ha soluzioni
viceversa
la soluzione $t_1=1/2$ tornando in x diventa
cosx=1/2 (vedi esercizio 1 fila A)
che ha soluzione

$x=+-pi/3+2kpi;$

OPPURE :

$(x=pi/3+2kpi)vv(x=5/3+2kpi)$

ESERCIZIO 9; FILA A

triangolo rettangolo: ipotenusa a=24, $alpha=30°$

esercizio del tipo "risoluzione di un triangolo rettangolo noti ipotenusa e un angolo"
Disegno del triangolo da risolvere:

Se ne deduce:

CATETO c (ipotenusa per il coseno dell'angolo non retto adiacente al cateto che si vuole calcolare)
c= a cos 30° = 24 cos 30° = 24 $sqrt(3)/2$ = 12 $sqrt(3)$
e
CATETO b (ipotenusa per il seno dell'angolo opposto al cateto che si vuole calcolare)
b= a sin 30° = 24 sin 30° = 24 $1/2$ = 12
e
$gamma=180°-alpha - beta= 180°-90°-30°=60°$

Verifica:(ha senso solo se non si e' usato Pitagora per trovare il secondo cateto):

$a^2 = b^2 + c^2 $ ?

$24^2 = $(12$sqrt(3))^2 #+# 12^2$

$24^2 = 144 * 3+ 144$

$24^2 = 144 *(3+1)$

$24^2 = 144 *(4)$

$(20+4)^2 = (100+40+4) * 4$

$400+160+16 = 400+160+16$
$(576=576)$ OK!

Quindi la risoluzione del triangolo rettangolo e' la seguente
a=24 ; b = 12 ; c=12 $sqrt(3)=(20.78) $
$alpha=90° beta=30° gamma=60°

ESERCIZIO 9; FILA B

triangolo rettangolo: ipotenusa a=12, $alpha=30°$

esercizio del tipo "risoluzione di un triangolo rettangolo noti ipotenusa e un angolo"
Disegno del triangolo da risolvere:

Se ne deduce:

CATETO c (ipotenusa per il coseno dell'angolo non retto adiacente al cateto che si vuole calcolare)
c= a cos 30° = 12 cos 30° = 12 $sqrt(3)/2$ = 6 $sqrt(3)$
e
CATETO b (ipotenusa per il seno dell'angolo opposto al cateto che si vuole calcolare)
b= a sin 30° = 12 sin 30° = 12 $1/2$ = 6
e
$gamma=180°-alpha - beta= 180°-90°-30°=60°$

Verifica (ha senso solo se non si e' usato Pitagora per trovare il secondo cateto):

$a^2 = b^2 + c^2 $ ?

$12^2 = $(6$sqrt(3))^2 #+# 6^2$

$144 = 36 * 3+ 36$

$144 = 36 *(3+1)$

$144 = (30+6) * 4$

$144 = 120+24$
$(144=144)$ OK!

Quindi la risoluzione del triangolo rettangolo e' la seguente
a=24 ; b = 6 ; c=6 $sqrt(3) = (10.39) $
$alpha=90° beta=30° gamma=60°

ESERCIZIO 10; FILA A

triangolo rettangolo: cateto b=15, $gamma=45°$

ESERCIZIO del tipo risoluzione di un triangolo rettangolo noti cateto e un angolo
Disegno del triangolo da risolvere:

Se ne deduce:

$beta=180°-alpha - gamma= 180°-90°-45°=45°$

Il triangolo e' isoscele: i due cateti sono lunghi uguale: c=15

Essendo $b=a cos(gamma)$
allora
$a= b/cos(gamma) = b/cos(45°) = b/((sqrt(2)/2)) = (2b) /sqrt(2) = (2b) /sqrt(2) * sqrt(2)/sqrt(2) = (2b sqrt(2))/2 = b sqrt(2) = 15sqrt(2) ~=21.21$

Se non abbiamo notato che il triangolo e' isoscele:

Calcoliamo $c=a cos(beta)$
allora
$c= a cos(beta) = a cos(45°) = [a] *(sqrt(2)/2) = [15(sqrt(2))] (sqrt(2)/2) = 15 (2/2) = 15$

Quindi la risoluzione del triangolo rettangolo e' la seguente

$a=15sqrt(2)$ ; b = 15 ; c=15
$alpha=90° beta=45° gamma=45°

ESERCIZIO 10; FILA B

triangolo rettangolo: cateto b=30, $gamma=45°$

ESERCIZIO del tipo risoluzione di un triangolo rettangolo noti cateto e un angolo
Disegno del triangolo da risolvere:

Se ne deduce:

$beta=180°-alpha - gamma= 180°-90°-45°=45°$

Il triangolo e' isoscele: i due cateti sono lunghi uguale: c=30

Essendo $b=a cos(gamma)$
allora
$a= b/cos(gamma) = b/cos(45°) = b/((sqrt(2)/2)) = (2b) /sqrt(2)= (60/sqrt(2)) = (2b) /sqrt(2) * sqrt(2)/sqrt(2) = (2b sqrt(2))/2 = b sqrt(2) = 30sqrt(2) ~=42.42$

Se non abbiamo notato che il triangolo e' isoscele:

Calcoliamo $c=a cos(beta)$
allora
$c= a cos(beta) = a cos(45°) = [a] *(sqrt(2)/2) = [30(sqrt(2))] (sqrt(2)/2) = 30 (2/2) = 30$

Quindi la risoluzione del triangolo rettangolo e' la seguente

$a=30sqrt(2)$ ; b = 30 ; c=30
$alpha=90° beta=45° gamma=45°

ESERCIZIO 11; FILA A

triangolo rettangolo: cateto b=4, cateto $c=4sqrt(3)$

ESERCIZIO del tipo risoluzione di un triangolo rettangolo noti due cateti
Disegno del triangolo da risolvere:

Calcoliamo l'ipotenusa

$a=sqrt(b^2+c^2)=$
$=sqrt((4)^2+(4sqrt(3))^2)=sqrt(16+16*3)=sqrt(16*(1+3))=sqrt(16*(4))=sqrt(16)*sqrt(4)=4*2=8$

Essendo $tg(beta)=b/c $ abbiamo
$ beta=tg^(-1)(b/c)=tg^(-1)((4)/(4sqrt(3)))=tg^(-1)(1/sqrt(3))=30°$$

dove ci siamo ricordati che:

$tg(30°)=sin(30°)/cos(30°)=((1/2))/((sqrt(3)/2))=(1/2)*(2/sqrt(3)) = 1/sqrt(3)$

Calcoliamo $gamma=180°-alpha°-beta=180°-90°-30°=90°-30°=60°$

La risoluzione del triangolo rettangolo e' pertanto:

$a=8$ ; $b = 4 $ ; $c=4 sqrt(3)$
$alpha=90° beta=30° gamma=60°

ESERCIZIO 11; FILA B

triangolo rettangolo: cateto b=8, cateto $c=8sqrt(3)$

ESERCIZIO del tipo risoluzione di un triangolo rettangolo noti due cateti
Disegno del triangolo da risolvere:

Calcoliamo l'ipotenusa

$a=sqrt(b^2+c^2)=$
$=sqrt((8)^2+(8sqrt(3))^2)=sqrt(64+64*3)=sqrt(64*(1+3))=sqrt(64*(4))=sqrt(64)*sqrt(4)=8*2=16$

Essendo $tg(beta)=b/c $ abbiamo
$ beta=tg^(-1)(b/c)=tg^(-1)((16)/(16sqrt(3)))=tg^(-1)(1/sqrt(3))=30°$$

dove ci siamo ricordati che:

$tg(30°)=sin(30°)/cos(30°)=((1/2))/((sqrt(3)/2))=(1/2)*(2/sqrt(3)) = 1/sqrt(3)$

Calcoliamo $gamma=180°-alpha°-beta=180°-90°-30°=90°-30°=60°$

La risoluzione del triangolo rettangolo e' pertanto:

$a=16$ ; $b = 8 $ ; $c=8sqrt(3)$
$alpha=90° beta=30° gamma=60°